La Société Française d’Ecologie (SFE) vous propose cette semaine le regard de Jean-Dominique Lebreton, Directeur de recherche au CNRS et Membre de l’Académie des Sciences, sur la dynamique des populations.
MERCI DE PARTICIPER à ces regards et débats sur la biodiversité en postant vos commentaires et questions après cet article. Les auteurs vous répondront et une synthèse des contributions sera ajoutée après chaque article.
———
Biodiversité et dynamique des populations
par Jean-Dominique Lebreton
Directeur de Recherche CNRS en Biologie des populations, Membre de l’Académie des Sciences
———
Mots clés : Populations, dynamique, mécanismes, taux de croissance, longévité, méthodes et outils, vertébrés, extinctions
———
Le chasseur paléolithique devait compter les rennes et l’apiculteur antique ses essaims avec la plus grande attention. Pourtant la dynamique des populations animales, et aussi végétales, s’est organisée beaucoup plus tard que la dynamique des populations humaines. Dès 1798, Malthus, si critiqué par ailleurs, soulignait ainsi à propos des populations humaines l’impossibilité d’une croissance exponentielle à l’infini.
Mais ce n’est que vers 1930 que les questions spécifiques aux populations animales sont clairement posées. La plus centrale concerne la relative stabilité des effectifs, comparée parfois à une simple houle à la surface de l’océan. Face aux variabilités de l’environnement et à la diversité des styles de vie, des arthropodes aux nombreuses générations annuelles aux tortues marines vivant peut-être plus d’un siècle, pourquoi et comment certaines populations fluctuent-elles plus que d’autres ? Comment opère la sélection naturelle ?
Pourquoi certaines espèces s‘éteignent-elles ? Lesquelles sont les plus sensibles à des perturbations ? Ces dernières questions prennent bien sûr une résonance toute particulière dans le contexte actuel des changements planétaires ; j’y reviendrai.
Des données démographiques par essence incomplètes
A la fin des années 60, le rôle inévitable du freinage démographique avec l’augmentation des effectifs (dit « densité dépendance »), souligné par David Lack, semble totalement masqué dans les études empiriques par les fortes variations environnementales des paramètres démographiques. Pour éclairer le jeu relatif des deux types de phénomènes, une interdisciplinarité quasi intrinsèque entre mathématique et biologie s’imposait. A de rares exceptions près, les tentatives de modélisation mathématique ou statistique butaient sur des spécificités mal prises en compte par les outils issus de la démographie humaine.

Une Mouette rieuse (Chroicocephalus ridibundus) sur son nid, marquée et identifiable par une combinaison unique de bagues colorées. Les réobservations ou recaptures d’individus marqués sont la principale source d’information démographique dans les populations animales. (© J-D. Lebreton)
Le premier obstacle est que personne n’est encore arrivé à forcer les mouettes, les orchidées ou les baleines à déclarer leurs naissances et leurs morts en mairie. En marquant des individus, et en suivant ces individus marqués, on pallie partiellement ce problème. Mais le suivi ne peut être exhaustif, et on ne peut donc utiliser sans dégâts les méthodes usuelles de table de vie. On accède en fait à un état civil partiel, comme un paysage vu à travers une passoire.
Ont donc été développés des modèles statistiques qui couplent aux paramètres d’intérêt biologique direct, comme les effectifs des populations (nombres d’individus) ou les probabilités de survie individuelle, des probabilités de détection ou de recapture rendant compte de l’incertitude inhérente à ces données de suivis d’individus marqués (cf. encart n°1). L’analyse statistique par ces méthodes dites de capture-marquage-recapture peut donc être vue pour une large part comme un traitement de signal. Il a fallu tout d’abord réorienter l’accent traditionnel de ces méthodes de l’estimation des effectifs vers l’estimation des paramètres démographiques, c’est-à-dire des flux d’individus. On a pu alors y introduire de manière féconde les idées de la régression linéaire et de l’analyse de variance. Il est ainsi devenu possible et courant d’estimer la mortalité dans des populations in natura, et de pouvoir décider de sa constance ou de sa variation avec la température hivernale, l’âge, le sexe, ou le statut reproducteur des individus.
Encart n°1 : Les méthodes de capture-marquage-recapture
Les méthodes de capture-marquage-recapture utilisent des suivis d’individus marqués pour estimer les effectifs des populations et divers paramètres démographiques.
Imaginons une population suivie chaque printemps pendant 8 ans. Un individu marqué la première année qui est mort entre la 6ème et la 7ème année aura une histoire que l’on peut noter 11111100, où 1 symbolise l’individu vivant, et 0 l’individu absent parce que mort. En pratique on ne peut cependant être certain de détecter tous les individus vivants, et l’histoire observée de cet individu sera par exemple 11010000. On peut seulement en conclure que l’individu est mort après 4 ans. Mais on sait aussi que cet individu, revu la quatrième année, était donc à coup sûr vivant la troisième alors qu’il n’a pas été capturé. Ce dernier type d’information va permettre d’estimer des « probabilités de recapture » qu’on appellera de façon plus générale «probabilités de détection ». En effet, très souvent la « capture » ne sera qu’une simple détection, à partir de caractéristiques utilisées comme marque individuelle non ambigüe : taches du pelage de lynx suivis par piégeage photographique, découpes de la queue de cétacés, ADN de loups obtenu à partir de leurs crottes, etc.

Identification sur son nid d’un pétrel à tête blanche, par le contrôle de sa bague (© Frédéric Jiguet, île Mayes, Kerguelen).
Dans notre exemple, si l’analyse des données de capture-recapture sur les 8 années indique que 200 individus marqués étaient encore vivants le troisième printemps (parce que détectés cette année là ou ultérieurement), et que 80 seulement ont été détectés ce troisième printemps, on peut estimer la probabilité de détection cette année-là par 80/200 = 0,400. Si l’on peut faire l’hypothèse qu’individus nouveaux (non marqués ou détectés pour la première fois) et individus marqués (ou déjà détectés) ont la même probabilité d’être détectés, on peut alors estimer l’effectif présent à partir de ces estimations des probabilités de détection. Ainsi, si au total on a détecté ce troisième printemps 400 individus (les 80 précédents, des individus non marqués et des individus déjà marqués mais pas revus ultérieurement), l’effectif peut être estimé par 400/0,400 = 1 000 individus.
De la même façon, une fois les probabilités de détection estimées, on peut corriger les taux de disparition pour estimer des taux de mortalité. Au cours des trente dernières années, ces méthodes de capture-marquage recapture se sont diversifiées et ont été généralisées à toutes sortes de situations, et permettent donc d’estimer des taux de mortalité (ou symétriquement de survie), de dispersion, d’accession à la reproduction, et de relier tous ces paramètres à des variables environnementales. Elles ont été appliquées à des milliers d’espèces animales, vertébrés mais aussi insectes. Elles ont été aussi appliquées à des plantes, par exemple pour estimer la mortalité d’espèces d’orchidées qui passent parfois une année « sous terre » sous forme de bulbes, bien vivantes donc, mais ne pouvant être détectées. Les méthodes de capture-marquage-recapture sont devenues ainsi un outil essentiel d’analyse des données issues de programmes à long terme, programmes qui apportent des informations de plus en plus précieuses sur les impacts des changements planétaires sur la biodiversité.
Un exemple me tient à cœur : c’est celui de la décroissance spectaculaire de la Cigogne blanche Ciconia ciconia en Alsace dès les années 60 (cf. schéma dans l’encart n°2). Cet exemple préfigure les questions concernant les conséquences biologiques des changements climatiques. En effet cette décroissance a pu être attribuée à une relation forte et directe entre mortalité et pluviométrie au Sahel, où les cigognes passent l’hiver, exonérant pour ainsi dire largement les changements environnementaux en Alsace même.
Réintégrées pleinement dans le giron de la Statistique, les méthodes de capture-marquage-recapture permettent désormais d’analyser finement les données de suivi individuel, basées de plus en plus sur des marques et des capteurs électroniques apportant des informations de plus en plus riches.
Un deuxième verrou était celui des modèles dynamiques : comment représenter un cycle de vie et des paramètres de naissance, mortalité, immigration et émigration, pour projeter les effectifs dans le temps ? Comment tenir compte de la saisonnalité presque universelle des cycles de reproduction, et de leur diversité ?
Comment « prédire » le devenir des populations ?
La projection inter-annuelle, pour déterminer la viabilité d’un phénotype ou d’une population, étant l’objectif principal, les modèles en temps discret, c’est-à-dire construits selon une échelle de temps discontinue et régulière, sont devenus l’outil de base. Ils tiennent compte de façon simple des différences universelles de performances démographiques avec l’âge (probabilité de survie annuelle, fécondité…), et de la complexité des cycles de vie. Le calcul matriciel et d’autres approches explicites permettent d’en comprendre finement le comportement ; leurs paramètres sont ceux des modèles statistiques de capture-recapture.

Maki catta (Lemur catta), lémurien malgache menacé d’extinction du fait de la destruction de son habitat forestier, photographié ici en captivité (© A. Teyssèdre)
Les généralisations les plus paradoxales concernent les modèles d’extinction de population. On s’intéresse alors à la probabilité d’extinction à long terme d’une population, et non plus à son taux de croissance, et l’intuition ordinaire est bien peu armée pour comprendre l’imbrication des effets déterministes et aléatoires, et son amplification par le décours du temps.
On appelle stochasticité démographique la variabilité irréductible qui fait que la mortalité se comporte comme une partie de pile ou face (cf. le regard n°9 d’Alexandre Robert sur cette plateforme). Dans un modèle sans autre effet, l’effectif à long terme est soit nul, soit infini. Pour engendrer une stabilisation des effectifs, il faut introduire par exemple une augmentation de mortalité avec l’augmentation des effectifs… Mais cette rétroaction, en empêchant les effectifs de diverger vers l’infini, rend alors l’extinction certaine à plus ou moins long terme… Paradoxe : en introduisant un mécanisme de persistance, on rend l’extinction certaine ! Il ne peut donc y avoir de stabilisation que conditionnellement à la non extinction.
Le paradoxe est finalement résolu en remarquant qu’une petite population relictuelle d’une dizaine d’individus peut avoir une probabilité d’extinction annuelle voisine par exemple de 0.05, et s’éteindra rapidement. Au contraire, une population de quelques centaines d’individus aura une probabilité d’extinction annuelle infiniment faible, par exemple 10 puissance moins 40. L’extinction reste certaine tout en étant de probabilité négligeable sur tout intervalle de temps fini.
En s’appuyant sur l’arsenal des processus stochastiques et de la dynamique des systèmes non linéaires, la modélisation en dynamique des populations est donc elle aussi rentrée dans le giron des mathématiques appliquées (cf. encadré n°2 ci-dessous). La dynamique des populations est ainsi devenue, pour reprendre un vers d’Aragon, « une tapisserie aux verdures banales », pleinement appropriée par les biologistes des populations. Les conséquences pour la biologie des populations ont été multiples. La dynamique des populations apporte notamment son éclairage sur ce qu’il est convenu d’appeler la crise de la biodiversité.
Pour la quasi-totalité des populations étudiées, les estimations de survie et d’âge de première reproduction ont été révisées vers le haut au cours des trente dernières années. Une conséquence immédiate est une révision à la hausse de la durée de génération, qu’on a donc pu enfin par le jeu conjoint des modèles statistiques et dynamiques, estimer correctement pour une large variété d’organismes.
Encart n°2 : Comment modéliser la dynamique d’une population ?
Dans le cas le plus simple d’une population isolée (sans immigration ni émigration), l’effectif de la population ne varie que sous l’effet des flux de naissance et de mort, comme un réservoir dont le niveau varie selon les flux d’entrée et de sortie. Chez beaucoup d’être vivants, la reproduction est annuelle, par exemple sous la forme d’un pic printanier en zone tempérée, et les modèles visant à comprendre et prédire les variations d’effectifs peuvent s’appuyer sur une échelle de temps dite « discrète », c’est-à-dire discontinue et régulièrement espacée. On s’intéresse par exemple à l’effectif avant le pic de reproduction chaque année : N(1), N(2),… N(t), N(t+1),…
On peut donc écrire N(t+1)=N(t)-décès + naissances. Si tous les individus se reproduisent à l’âge d’un an, et donnent naissance à f individus, qui survivent en proportion S1 jusqu’au printemps suivant, le nombre d’entrées dans la population est simplement N(t) x f x S1. Si les individus de plus d’un an survivent en proportion S, le nombre de décès est simplement N(t) x (1-S) et on obtient N(t+1) = (S + f x S1) N(t). Derrière cette équation se flushnt déjà diverses hypothèses (constance des paramètres au cours du temps, pleine reproduction à un an…) et quelques pièges : dans le cas d’une reproduction sexuée, la fécondité f est celle d’un couple d’individus, et on restreindra le modèle au nombre de femelles dans la population ; il ne faut donc pas oublier d’exprimer f en femelles nouvelles-nées par femelle reproductrice pour ne pas surestimer la fécondité. En revenant à l’équation N(t+1) = (S + f x S1) N(t), on voit donc que la population est multipliée chaque année par a = S + f x S1. Chez un petit passereau comme la mésange bleue, avec par exemple S =0,5, S1= 0,2 et f= 4, a = 0,5 + 4*0,2 = 1,3. Le modèle prédit donc une croissance exponentielle à un rythme de 30 % par an. Si a avait été plus petit que 1, la population modélisée aurait été en décroissance.
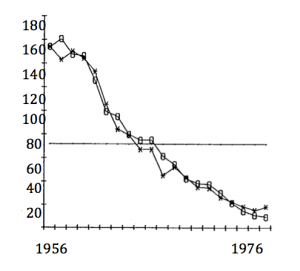
Reconstitution par un modèle démographique (symboles évidés) des effectifs nicheurs de Cigogne blanche au Bade-Wurtemberg (croix) pendant une phase de décroissance. Dans ce modèle la mortalité annuelle varie de façon directe avec une mesure de pluviométrie sur les lieux d’hivernage des Cigognes au Sahel, dans une relation validée par une analyse de capture-recapture. (Travaux de S. Kanyamibwa et coll., 1992)
Pour des cycles de vie plus complexes, lorsque l’accession à la reproduction ne se fait que de façon échelonnée avec l’âge, ou lorsque l’on considère plusieurs sites, la population est « structurée » et il faut considérer plusieurs composantes de l’effectif à chaque date : par classe d’âge, par site… On alors plusieurs équations, et des outils mathématiques plus complexes sont nécessaires pour analyser le comportement du modèle, principalement le calcul matriciel. Si les paramètres sont constants, la croissance à un taux fixe – croissance exponentielle donc comme celle d’un capital placé à un taux fixe – reste la règle, à un détail près : il faut que la population « oublie » sa structure d’âge et/ou spatiale initiale, qui peut temporairement l’écarter assez notablement de son régime de croissance à long terme. Imaginez une opération de réintroduction d’une espèce menacée dans laquelle on ne relâche que des individus immatures : tant qu’une fraction suffisante des individus n’a pas commencé à se reproduire, la population ne peut que décroître, puisqu’il n’y a temporairement que des décès. Elle n’atteindra son régime de croissance « de croisière » qu’après un temps de latence.
Ce type de modèle peut aussi être généralisé à l’aide de lois de probabilité laissant place au hasard, dans des modèles dit « stochastiques », par opposition aux modèles précédents dits « déterministes », pour étudier les risques d’extinction de populations. Ces mathématiques parfois complexes ne sont là qu’au service de la biologie, suivant le mot du grand biologiste J.B.S. Haldane : « Face à une difficulté ou controverse scientifique, une once d’algèbre vaut une tonne de discours. » (« If you are faced by a difficulty or a controversy in science, an ounce of algebra is worth a ton of verbal argument »).
Longévité des individus et vulnérabilité des populations
La durée de génération, définie comme l’âge moyen des mères lors des naissances de leurs enfants, est une excellente mesure de la longévité reproductive. Elle a peu retenu l’attention des démographes humains, parce qu’elle varie peu entre populations humaines, au grand maximum d’un facteur 1 à 2. À l’échelle des Vertébrés, elle varie dans un rapport de 1 à 300, de quelques dizaines de jours chez les micromammifères à des dizaines d’années chez certains oiseaux de mer ou les grands cétacés. Or, par le jeu de l’étalement de l’investissement de reproduction sur la vie entière de l’individu, la durée de génération est directement liée aux capacités de croissance de la population.
Chez les oiseaux et les mammifères, le taux de croissance maximum d’une population est ainsi voisin de l’inverse de la durée de génération. Or ce taux de croissance maximum, c’est aussi le taux maximum de prélèvement ou de surmortalité que peut supporter une espèce. Par exemple une population d’albatros avec une durée de génération de 25 ans ne peut guère croître à plus de 4 % par an, et donc supporter plus de 4% de captures accidentelles par les hameçons de la pêche palangrière.
Les vertébrés homéothermes ont donc une durée de génération beaucoup plus élevée qu’on le croyait il y a seulement vingt ans. Le « taux d’intérêt » que représente leur taux de croissance maximum est donc plus faible qu’on ne le croyait. Comme un capital placé à un faible taux d’intérêt, il n’est donc pas surprenant qu’ils supportent très mal l’impôt des activités humaines. Les efforts de protection de grands vertébrés comme l’Ours brun ou le Condor de Californie, ou demain, l’Ours blanc et le Manchot empereur sont donc justifiés non parce que ces grands vertébrés sont emblématiques, mais parce qu’ils sont longévifs. De fait la longévité et la taille corporelle qui lui est fortement corrélée sont effectivement de bons prédicteurs du risque d’extinction. Que l’on parle d’albatros, de baleines, de tortues marines ou de séquoias, il y a donc véritablement une malédiction des espèces longévives.
Environ 50 000 espèces de vertébrés peuplent notre planète aujourd’hui, et nous en perdons au moins une par an depuis plus de 400 ans. A ce rythme, toutes seraient éteintes d’ici 50 000 ans : l’échelle de temps fera sourire le géologue et l’homme politique, pour des raisons diamétralement opposées.
Les recherches continuent
La dynamique des populations est encore en rapide évolution, avec des défis méthodologiques comme l’intégration d’informations multiples dans un cadre de modélisation unique. Les défis empiriques concernent aussi bien la biologie évolutive, par exemple l’évolution de la dispersion, que la compréhension des effets des changements planétaires sur la biodiversité. De ce point de vue, la dynamique des populations d’arthropodes, eux-mêmes souvent inféodés à des végétaux à grande durée de génération, et la compréhension de leurs risques d’extinction constituent une des grandes questions. La poursuite du développement d’une dynamique des populations comparée, dont participent mes réflexions sur la durée de génération, en est une autre.
Bibliographie
Kanyamibwa S. et J-D. Lebreton, 1992. Variation des effectifs de cigogne blanche et facteurs de milieu: un modèle démographique. pp. 259-264 in Les cigognes d’Europe, Mériaux J.L., Schierer A., Tombal C. & J-C. Tombal, Eds. Institut Européen d’Ecologie, Metz.
Lebreton J-D., Almeras T. et R. Pradel, 1999. Competing events, mixtures of information and multistrata recapture models, Bird Study, 46 (supplement), pp. 39- 46.
Lebreton J-D., Burnham K. P., Clobert J. et D.R. Anderson, 1992. Modeling survival and testing biological hypotheses using marked animals: a unified approach with case studies, Ecological Monographs, 62, pp. 67 – 118.
Lebreton J.-D., Nichols J.D., Barker R.J., Pradel R. & J.A. Spendelow, 2009. Modeling individual animal histories with multistate capture-recapture models. Advances in Ecological Research, 41: 87-173.
Lebreton J-D. et P.M. North, eds., 1993. Marked individuals in the study of bird population. Birkhaüse Verlag, Basel.
Regards sur des sujets voisins, en ligne sur cette plateforme :
Olivieri, 2013. Evolution, adaptation, spéciation… Regard sur la biodiversité, l’évolution et la recherche. Regards et débats sur la biodiversité, SFE, Regard n°42, 22 février 2013.
Robert A., 2011. Petites populations et vortex d’extinction. Regards et débats sur la biodiversité, SFE, Regard n°9, 10 janvier 2011.
Ce « regard » est une version adaptée et complétée pour cette plateforme du discours d’entrée de l’auteur à l’Académie des Sciences,
éditée par Anne Teyssèdre.
——



Bonjour Jean-Dominique,
Merci pour ce regard instructif sur la dynamique des populations, qui n’est peut-être pas très explicite cependant pour les non avertis. Pourrais-tu expliciter un peu la méthode de capture-marquage-recapture, et son principe ? : Comment cette méthode permet-elle de calculer les effectifs des populations et les probabilité de survie des individus, ainsi que les « flux » d’individus ? Peut-elle prendre en compte les déplacements migratoires (émigrations et immigrations) d’une partie des individus, et comment ?
Bien cordialement,
Anne
Ajout du 30 mai : Les réponses de l’auteur à cette question et à la question suivante forment un complément un peu technique intéressant pour les non spécialistes. C’est pourquoi je les ai insérées dans l’article ci-dessus, sous la forme de deux encarts.
Bonjour Anne,
Les méthodes de capture-marquage-recapture utilisent des suivis d’individus marqués pour estimer les effectifs des populations et divers paramètres démographiques. Imaginons une population suivie chaque printemps pendant 8 ans. Un individu marqué la première année qui est mort entre la 6ème et la 7ème année aura une histoire que l’on peut noter 11111100, où 1 symbolise l’individu vivant, et 0 l’individu absent parce que mort. En pratique on ne peut cependant être certain de détecter tous les individus vivants, et l’histoire observée de cet individu sera par exemple 11010000. On peut seulement en conclure que l’individu est mort après 4 ans. Mais on sait aussi que cet individu, revu la quatrième année, était donc à coup sûr vivant la troisième alors qu’il n’a pas été capturé. Ce dernier type d’information va permettre d’estimer des « probabilités de recapture » qu’on appellera de façon plus générale «probabilités de détection ». En effet, très souvent la « capture » ne sera qu’une simple détection, à partir de caractéristiques utilisées comme marque individuelle non ambigüe : taches du pelage de lynx suivis par piégeage photographique, découpes de la queue de cétacés, ADN de loups obtenu à partir de leurs crottes, etc…
Dans notre exemple, si l’on sait que par exemple que 200 individus étaient vivants le troisième printemps, et qu’on en a détecté seulement 80, on peut estimer la probabilité de détection cette année-là comme égale à 80/200 = 0,400. Si l’on peut faire l’hypothèse qu’individus nouveaux (non marqués ou détectés pour la première fois) et individus marqués (ou déjà détectés) ont la même probabilité d’être détectés, on peut alors estimer l’effectif présent. En effet si au total on a détecté ce troisième printemps 400 individus (y compris les 80 connus pour être vivants), l’effectif peut être estimé par 400/0,400 = 1 000 individus.
De la même façon, une fois les probabilités de détection estimées, on peut corriger les taux de disparition pour estimer des taux de mortalité. Au cours des trente dernières années, ces méthodes de capture-marquage recapture se sont diversifiée et ont été généralisées à toutes sortes de situations, et permettent donc d’estimer des taux de mortalité (ou symétriquement de survie), de dispersion, d’accession à la reproduction, et de relier tous ces paramètres à des variables environnementales. Elles ont été appliquées à des milliers d’espèces animales, vertébrés mais aussi insectes. Elles ont été aussi appliquées à des plantes, par exemple pour estimer la mortalité d’espèces d’orchidées qui passent parfois une année « sous terre » sous forme de bulbes, bien vivantes donc, mais ne pouvant être détectées. Les méthodes de capture-marquage-recapture sont devenues ainsi un outil essentiel d’analyse des données issues de programmes à long terme, programmes qui apportent des informations de plus en plus précieuses sur les impacts des changements planétaires sur la biodiversité.
Autre question, pour éclairer les non écologues : Pourrais-tu expliquer brièvement comment la saisonnalité de la reproduction (reproduction annuelle chez de nombreux organismes), et la variation de la probabilité de survie individuelle avec l’âge, sont prises en compte dans les modèles de dynamique des populations ? (Structuration des populations par classes d’âge, progression par pas de temps, …)
Dans le cas le plus simple d’une population isolée (sans immigration ni émigration), l’effectif de la population ne varie que sous l’effet des flux de naissance et de mort, comme un réservoir dont le niveau varie selon les flux d’entrée et de sortie. Chez beaucoup d’être vivants, la reproduction est annuelle, par exemple sous la forme d’un pic printanier en zone tempérée, et les modèles visant à comprendre et prédire les variations d’effectifs peuvent s’appuyer sur une échelle de temps dite « discrète », c’est-à-dire discontinue et régulièrement espacée. On s’intéresse par exemple à l’effectif avant le pic de reproduction chaque année : N(1), N(2),… N(t), N(t+1),…
On peut donc écrire N(t+1)=N(t)-décès + naissances. Si tous les individus se reproduisent à l’âge d’un an, et donnent naissance à f individus, qui survivent en proportion S1 jusqu’au printemps suivant, le nombre d’entrées dans la population est simplement N(t) x f x S1. Si les individus de plus d’un an survivent en proportion S, le nombre de décès est simplement N(t) x (1-S) et on obtient N(t+1) = (S + f x S1) N(t). Derrière cette équation se flushnt déjà diverses hypothèses (constance des paramètres au cours du temps, pleine reproduction à un an…) et quelques pièges : dans le cas d’une reproduction sexuée, la fécondité f est celle d’un couple d’individus, et on restreindra le modèle au nombre de femelles dans la population ; il ne faut donc pas oublier d’exprimer f en femelles nouvelles-nées par femelle reproductrice pour ne pas surestimer la fécondité. En revenant à l’équation N(t+1) = (S + f x S1) N(t), on voit donc que la population est multipliée chaque année par a = S + f x S1. Chez un petit passereau comme la mésange bleue, avec par exemple S =0,5, S1= 0,2 et f= 4, a = 0,5 + 4*0,2 = 1,3 : le modèle prédit donc une croissance de 30 % par an. Si a avait été plus petit que 1, la population modélisée aurait été en décroissance.
Pour des cycles de vie plus complexes lorsque l’accession à la reproduction ne se fait que de façon échelonnée avec l’âge, ou lorsque l’on considère plusieurs sites, la population est « structurée » et il faut considérer plusieurs composantes de l’effectif à chaque date : par classe d’âge, par site… On alors plusieurs équations, et des outils mathématiques plus complexes sont nécessaires pour analyser le comportement du modèle, principalement le calcul matriciel. Si les paramètres sont constants, la croissance à un taux fixe, croissance exponentielle donc comme celle d’un capital placé à un taux fixe reste la règle, à un détail près : il faut que la population « oublie » sa structure initiale, qui peut temporairement l’écarter assez notablement de son régime de croissance à long terme : imaginez une opération de réintroduction d’une espèce menacée dans laquelle on ne relâche que des individus immatures : tant qu’une fraction suffisante des individus n’a pas commencé à se reproduire, la population ne peut que décroître, puisqu’il n’y a temporairement que des décès.
Ce type de modèle peut aussi être généralisé à l’aide de lois de probabilité, dans des modèles dit « stochastiques », par opposition aux modèles précédents dits « déterministes », pour étudier les risques d’extinction de populations. Ces mathématiques parfois complexes ne sont là qu’au service de la biologie, suivant le mot du grand biologiste J.B.S. Haldane : « if you are faced by a difficulty or a controversy in science, an ounce of algebra is worth a ton of verbal argument ».
Bonjour,
Ces deux réponses de l’auteur ont leur place dans l’article ci-desssus. Avec l’accord de Jean-Dominique, je vais les éditer et les placer sous forme d’encarts dans ce « regard » sur la dynamique des populations.
(Encarts mis en ligne le 29 mai.)
Anne
Bonjour,
Je me présente, Ange Mury. Mon sujet de thèse porte sur la dynamique de population de tortues grecques (Testudo Graeca) dans une région du Maroc nommée le Moyen Atlas. Ma question est de savoir quelles études on peut faire, à partir de la méthode capture-marquage-recapture, pour élaborer la structure démographique d’une population. Pourriez-vous me conseiller au plan bibliographique (un livre, ou chapitre de livre sur le sujet) ?
Cordialement,
A. Mury
Les naissances et les morts des tortues que vous étudiez ne sont pas consignées dans des registres d’état-civil, comme c’est le cas dans les populations humaines. En marquant les individus, et en les réobservant ou les recapturant , vous pouvez cependant obtenir l’équivalent d’un état-civil. Simplement comme ces réobservations ou ces recaptures ne peuvent être exhaustives, vous allez inévitablement manquer des individus de temps à autre. Les méthodes statistiques de capture-recapture permettent précisément de tenir compte de ces « trous » dans les données et d’estimer néanmoins la mortalité, mais aussi d’estimer la proportion d’individus nouveaux dans la population, et donc le degré de renouvellement des individus.
L’identification des individus par une marque propre à chaque individu permet de les suivre au cours du temps : on parle de données « longitudinales », par opposition par exemple au recueil d’une structure d‘âge, pour lequel on parle de données « transversales ». L’obtention de données longitudinales est décisif pour comprendre la dynamique de populations, car l’analyse de ces données permet de comprendre le rôle relatif de la fécondité, de la mortalité, voire de l’immigration et de l’émigration d’individus.
La mise en œuvre des méthodes de capture-recapture est facilitée par l’existence de logiciels puissants et conviviaux. Des stages de formation à ces méthodes sont régulièrement organisés par diverses équipes dans le monde, car il reste néanmoins difficile de se former par soi-même, l’entreprise, de la planification du recueil des données à l’analyse de ces données en passant par le travail de terrain, étant fortement pluridisciplinaire. Un mes meilleurs ouvrages pour acquérir une vue d’ensemble est le livre de Byron K. Williams, James D. Nichols et Michael J. Conroy, intitulé « Analysis and management of animal populations », publié en 2001 par Academic Press.